Drawing an Isosceles Right Triangle
Here is a fun way for intermediate students to use coding and the GO robot to construct, identify, classify, and measure 2 dimensional figures. This activity explores some of the geometry and measurement standards relating to angles, triangles, and perpendicular lines. See CCSS: 4.G.A.1 & 2 and 4.MD.C.7, as examples.
- Build the GO Code Base and add a standard dry erase marker to the front using 2 green angle beams, 2 yellow connectors, 2 green pins, 1 red pin, and a rubber band.
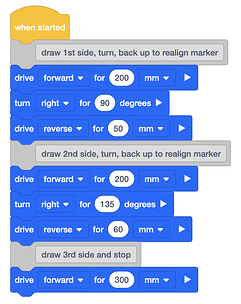
- Create a project in VEX GO to draw an isosceles triangle with two 45 degree angles and one right angle. My sample code is below. Since the marker is 30 mm in front of the center of the wheel base, it is not the center of the turning radius of the Code Base. I added in the “reverse” distances to realign the marker so it is touching the last completed line before it starts the next line. I ran iterations with various distances until I was happy with the way my finished triangle looked. For the first angle, the robot turns right 90 degrees. For the 2nd angle, the code is measuring the outside angle of 135 degrees for the desired inside angle of 45 degrees.
- Pair the brain and run the project, see linked video.
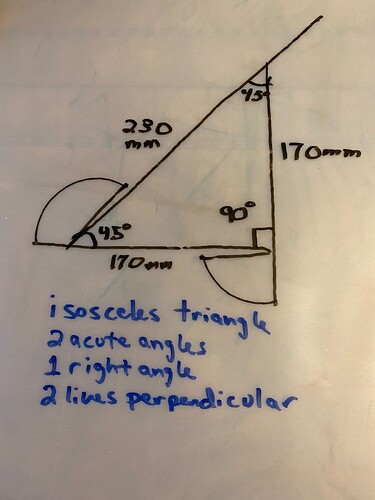
Drawing an Isosceles Triangle - Use a ruler and protractor to measure the angles and side lengths to see how they compare to the angles and lengths that were coded.
- My actual angles were within 2 degrees of 45 and 90 degrees. Since the center of the marker was 30 mm in front of the center of the wheel base, the 2 triangle legs were 30 mm shorter than the coded length. In the drawing, these 2 legs measured 170 mm, while the code is to “drive forward for 200 mm”. The extra 30 mm is shown in the extension of the line where the robot turns and reverses to realign itself. This code produces a triangle with 2 congruent side lengths, 2 acute angles, and 1 right angle (2 perpendicular lines).
- This example is done in millimeters. A comparison of inches and millimeters/centimeters could be added to incorporate another measurement standard (CCSS 2.MD.A.2).
- This could be an open-ended assignment in which students decide the combination of angle types and side lengths, then answer questions about their construction. Happy creating!