Hello everyone! I was inspired by the IQ Wheel Turns Activity and it got me thinking about common questions I used to hear from students all the time, such as “what is Pi?” or “what is circumference and diameter?”
To help students explore circumference, diameter and ultimately what Pi is, I came up with this activity that I’m going to share! ![]()
I took three different sized V5 wheels, the 2.75", the 3.25" and the 4".
I then measured the diameter of each wheel in millimeters. You can use any standard measuring device or the Metal Parts Ruler.
Next, I measured how far one wheel turn is for each sized wheel. One wheel turn is the equivalent to the circumference of the wheel. To do this, I marked with tape a line on the wheel, set up that point at the beginning of the ruler, rolled the wheel one full turn (or revolution) until the same point touched the ruler again and recorded the measurement. You can also mark the start and end locations on a piece of paper and then measure the distance in between them.
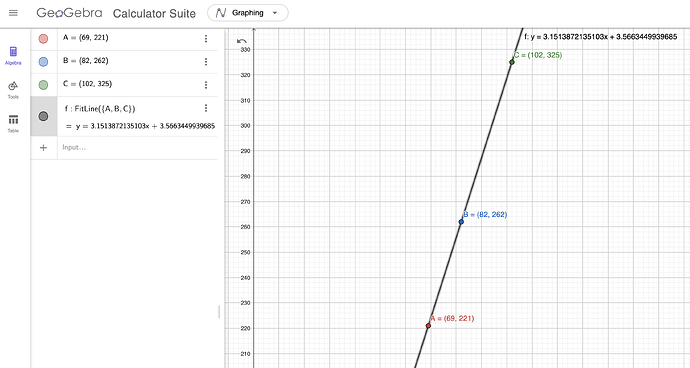
Once I did that for each of the three wheels, I took my data and plotted it using GeoGebra software. Then, I had the software generate the line of best fit for all three data points. The equation of the best fit line had a slope of approximately 3.15. This is representing Pi!
Students can also divide each circumference measurement by the accompanying diameter measurement to see that even individually with each data point, the ratio is close to 3.14. For example, 325/102 = 3.18
So what exactly does this mean? This means that Pi is the constant, it’s the ratio of the circumference to the diameter. Of every single circle, no matter the size. Mind blowing, I know! Doing this activity helps students conceptually understand what Pi is, instead of this crazy number that students just want to see how many digits they can memorize.
If I were doing this activity in a classroom, I would then ask students to write an equation that represents the relationship between, circumference, diameter, and Pi.
Most students would probably write something such as, Pi = circumference / diameter.
Then, if you ask them to just solve for circumference, you get circumference = Pi times diameter, which is the formula for circumference! Doing this activity allows students to derive the formula themselves, instead of just handing them a formula and asking them to complete procedural problems (plug and chug).
Now, something to consider with this activity is that of course the ratios will not be perfect as measurement can account for human error and it’s not as precise. This is a great discussion point to bring up with students. Why do we have this formula? Well, some circles are really really big and round (like the earth… lol). Measuring non-linear distances (curves) is difficult, so we can use a formula. Using the formula also allows for more precision.
Let me know what you think of this activity! How could you use or adapt this in your classroom? ![]()